Asymptotic Notations Explained

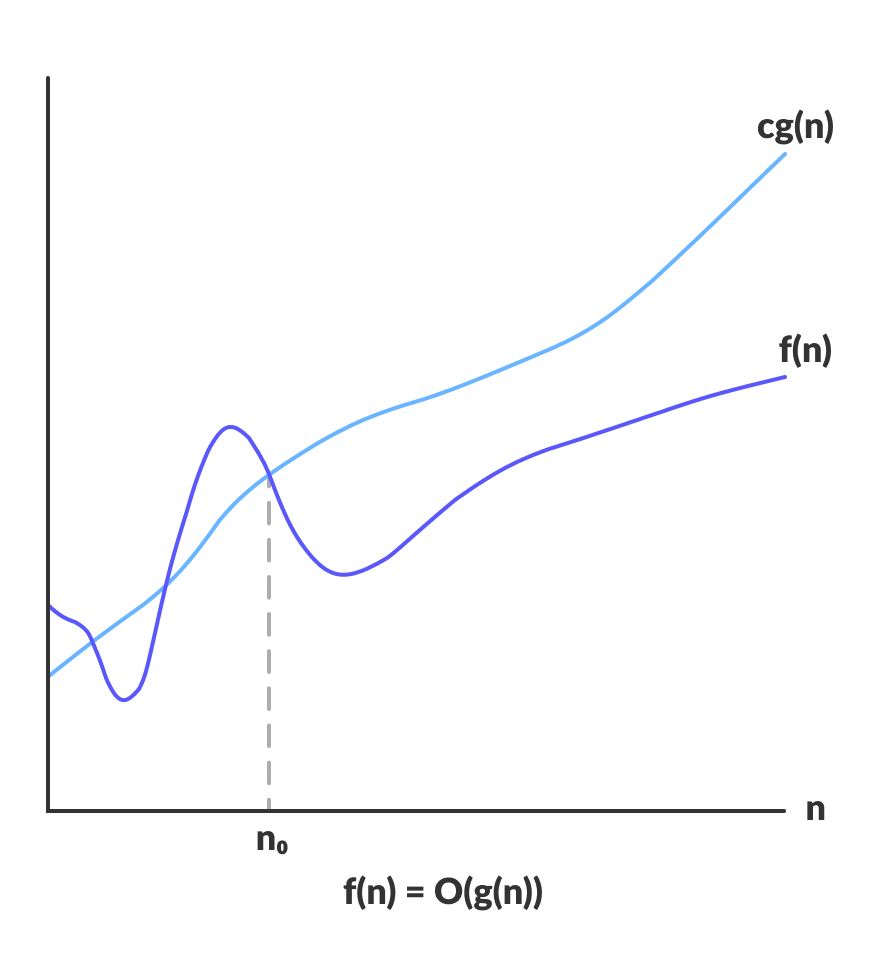
1. Big O Notation – O (Upper Bound)

Big O Notation tells the Worst-Case performance of an algorithm. It is also known as the Upper Bound.

  • Meaning: It guarantees that the algorithm’s running time will never go above a certain limit. It shows how slow the algorithm can be in the worst case.
  • On Graph:
    • If a function f(n) has a time complexity O(g(n)), it means that after a point (n₀), f(n) will always remain below or on the line c · g(n).
    • Formula: f(n) ≤ c · g(n) for all n ≥ n₀
  • Example: If we say Quick Sort has a Worst-Case complexity of O(n²), it means its growth will not exceed n².
Big O Graph

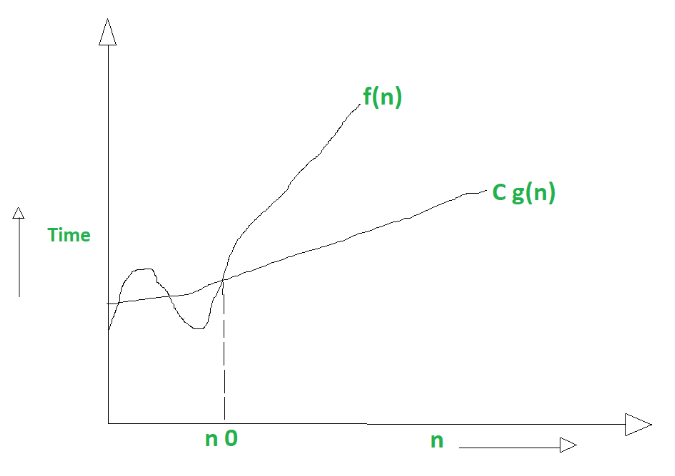
2. Omega Notation – Ω (Lower Bound)

Omega Notation tells the Best-Case performance of an algorithm. It is also called the Lower Bound.

  • Meaning: It guarantees that the algorithm’s running time will never go below a certain limit. It represents how fast the algorithm can be.
  • On Graph:
    • If a function f(n) has a time complexity Ω(g(n)), it means that after a point (n₀), f(n) will always remain above or on the line c · g(n).
    • Formula: f(n) ≥ c · g(n) for all n ≥ n₀
  • Example: Quick Sort’s Best-Case complexity is Ω(n log n). This means it will not run faster than n log n.
Omega Graph

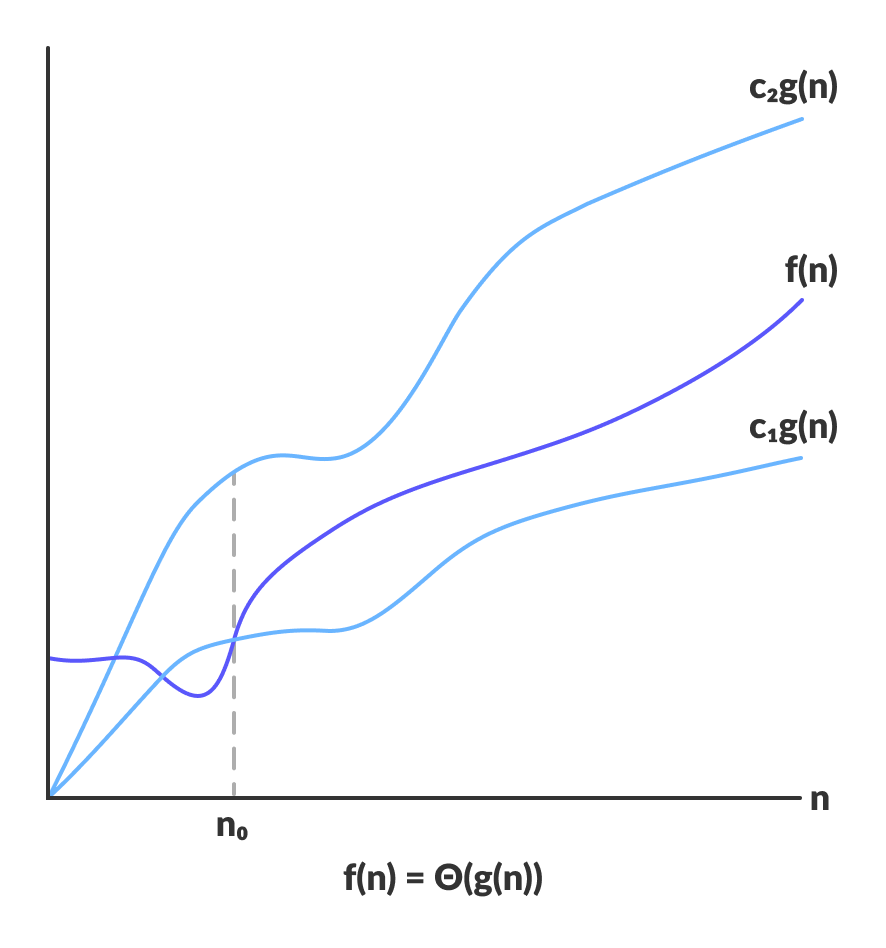
3. Theta Notation – Θ (Tight Bound)

Theta Notation represents the Average-Case or Exact Asymptotic Behavior of an algorithm. It is also known as the Tight Bound.

  • Meaning: It is the most precise notation. It guarantees that the algorithm’s running time will lie between two functions (c₁ · g(n) and c₂ · g(n)). This means the growth rate in both best and worst cases is almost the same.
  • On Graph:
    • If a function f(n) has a time complexity Θ(g(n)), then after a point (n₀), f(n) will always remain between c₁ · g(n) and c₂ · g(n>.
    • Formula: c₁ · g(n) ≤ f(n) ≤ c₂ · g(n) for all n ≥ n₀
  • Example: Merge Sort always has a complexity of Θ(n log n). This means its running time will always stay around n log n.
Theta Graph

Summary

Notation Big O (O) Omega (Ω) Theta (Θ)
Meaning Upper Bound Lower Bound Tight Bound
Case Worst-Case Best-Case Average-Case
Simple Meaning Will never exceed this Will never go below this Will stay around this

These notations help us understand how an algorithm grows or slows down when the input size increases.

Comments

Post a Comment

Popular posts from this blog

Data Abstraction

Image
What is Data Abstraction? Data Abstraction ka matlab hota hai: “Sirf zaruri cheez dikhana, aur jo andar ki complex working hai usse chhupa dena.” Programming me hum user ko sirf “What to do” dikhate hain aur “How to do it” chhupa lete hain. Isse system simple, secure aur easy-to-use ban jaata hai.     Real-Life Example: TV Remote TV Remote abstraction ka perfect example hai. Aap remote me bas Volume Up , Channel Change , Power jaisa button dabate ho. Aapko nahi pata hota ki andar circuit kaise signal create karta hai, TV tak kaise pahuchta hai, software usse kaise process karta hai. Aapko sirf zaruri functionality dikh rahi hai → This is Abstraction! Agar company remote ki chip badal bhi de, aapka use karna same hi rahta hai. Programming Me Data Abstraction Coding me Data Abstraction ka matlab hota hai ki hum classes aur functions ko aise design karein ki: User ko sirf use karne layak functions dikhaye dein. Un functions ke andar kya logic chal raha hai, woh poora hid...
Read more

Data Abstraction

Image
  What is Data Abstraction? Data Abstraction means showing only the important information to the user and hiding all the internal working details. In simple words: Show what to do . Hide how it works . This makes a system easy to use, clean, and less confusing.   Real-Life Example: TV Remote When you use a TV remote: You only press buttons like Volume Up, Volume Down, or Channel Change. You do not see how the signal travels inside the remote, how the chip works, or how the TV processes the signal. You only see the basic functions. The internal working is hidden. This is called Abstraction . Data Abstraction in Programming In programming, abstraction means that: The user only sees the required functions or methods. The logic inside those functions remains hidden. Example: When you call saveData(data) in a program: You only know that the data will be saved. You do not know whether it is saved using SQL, NoSQL, a file system, or something else. The internal process is hidden fro...
Read more

Data Structure Ka Parichay Aur Prakar (Introduction and Types of Data Structure)

Image
  1. Data Structure Ki Definition Data Structure ek logical aur systematic tareeka hai jisme data elements ko organize kiya jata hai taki essential operations jaise search, add aur delete efficiently kiye ja sake kam time aur memory mein. Simple Example: Ek library ko consider karo. Books (data) ko shelves (data structures) mein unke subjects ke hisaab se arrange kiya jata hai, taki jab aap koi book dhundho to turant mil jaye. 2. Data Structures Ke Prakar Data Structures mainly do categories mein divide hote hain: Primitive aur Non-Primitive . A. Primitive Data Structures Ye basic data types hote hain jo directly machine level par kaam karte hain. Programming languages inhe pre-defined provide karti hain. Integer (int): Poorn sankhyaon ko store karta hai. Example: 10, -5, 1000 Float/Double: Dashmlav sankhyaon ko store karta hai. Example: 3.14, 0.005 Character (char): Single akshar ya symbol store karta hai. Example: 'A', 'z', '9' Boolean (bo...
Read more