Explain Asymptotic Notations – Big O, Ω, Θ with graphs

Asymptotic Notations Explained

1. Big O Notation (बिग ओ नोटेशन) - O (Upper Bound)

Big O Notation किसी एल्गोरिथ्म की Worst-Case (सबसे खराब स्थिति) की performance को बताता है। इसे Upper Bound (ऊपरी सीमा) भी कहते हैं।

  • मतलब: यह गारंटी देता है कि एल्गोरिथ्म का Running Time एक लिमिट से कभी भी ऊपर नहीं जाएगा (उससे ज़्यादा नहीं होगा)। यह बताता है कि यह सबसे धीमा (slowest) कितना हो सकता है।
  • ग्राफ पर:
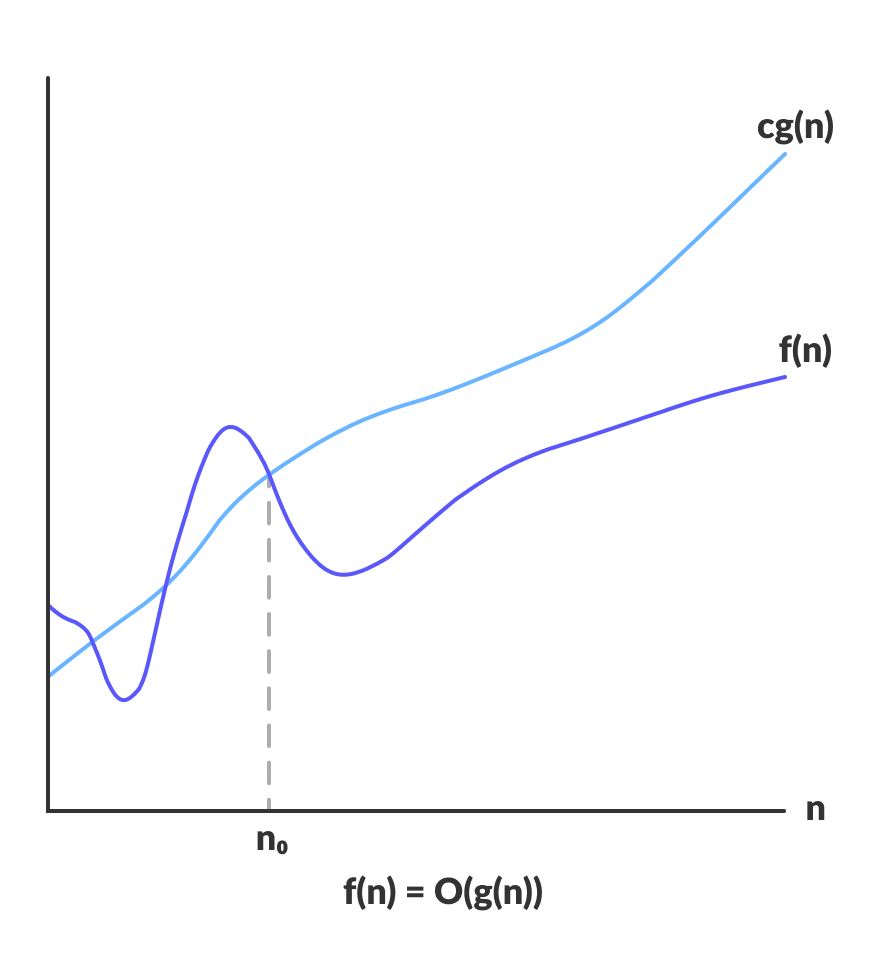
    • अगर किसी फंक्शन f(n) का टाइम कॉम्प्लेक्सिटी O(g(n)) है, तो इसका मतलब है कि एक पॉइंट (n₀) के बाद, f(n) हमेशा c · g(n) वाली लाइन से नीचे या उस पर रहेगा।
    • Formula: f(n) ≤ c · g(n) for all n ≥ n₀
  • Example: अगर हम कहें कि Quick Sort की Worst-Case कॉम्प्लेक्सिटी O(n²) है, तो इसका मतलब है कि यह n² से तेजी से नहीं बढ़ेगा।
Big O Graph

2. Omega Notation (ओमेगा नोटेशन) - Ω (Lower Bound)

Omega Notation किसी एल्गोरिथ्म की Best-Case (सबसे अच्छी स्थिति) की performance को बताता है। इसे Lower Bound (निचली सीमा) भी कहते हैं।

  • मतलब: यह गारंटी देता है कि एल्गोरिथ्म का Running Time एक लिमिट से कभी भी नीचे नहीं जाएगा (उससे कम नहीं होगा)। यह बताता है कि यह सबसे तेज़ (fastest) कितना हो सकता है।
  • ग्राफ पर:
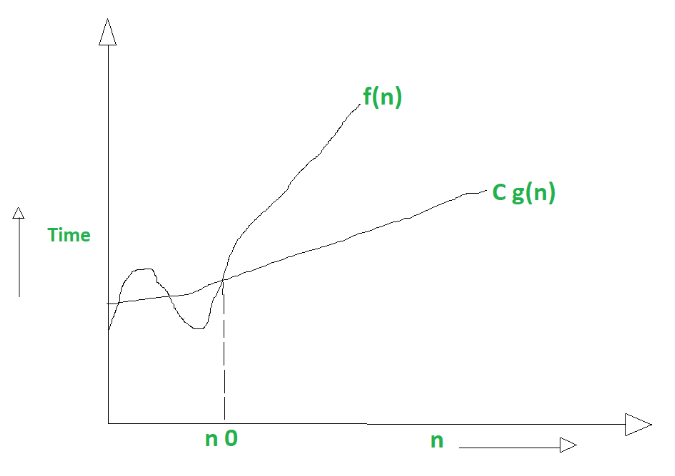
    • अगर किसी फंक्शन f(n) का टाइम कॉम्प्लेक्सिटी Ω(g(n)) है, तो इसका मतलब है कि एक पॉइंट (n₀) के बाद, f(n) हमेशा c · g(n) वाली लाइन से ऊपर या उस पर रहेगा।
    • Formula: f(n) ≥ c · g(n) for all n ≥ n₀
  • Example: Quick Sort की Best-Case कॉम्प्लेक्सिटी Ω(n log n) होती है। इसका मतलब है कि यह n log n से धीमा नहीं होगा (यानी इससे कम टाइम नहीं लेगा)।
Omega Graph

3. Theta Notation (थीटा नोटेशन) - Θ (Tight Bound)

Theta Notation किसी एल्गोरिथ्म की Average-Case (औसत स्थिति) या Exact Asymptotic Behavior को बताता है। इसे Tight Bound (सख्त सीमा) भी कहते हैं।

  • मतलब: यह सबसे Precise (सटीक) Notation है। यह गारंटी देता है कि एल्गोरिथ्म का Running Time दो फंक्शन्स (c₁ · g(n) और c₂ · g(n)) के बीच में फंसा रहेगा। इसका मतलब है कि Best-Case और Worst-Case दोनों का ग्रोथ रेट एक जैसा है।
  • ग्राफ पर:
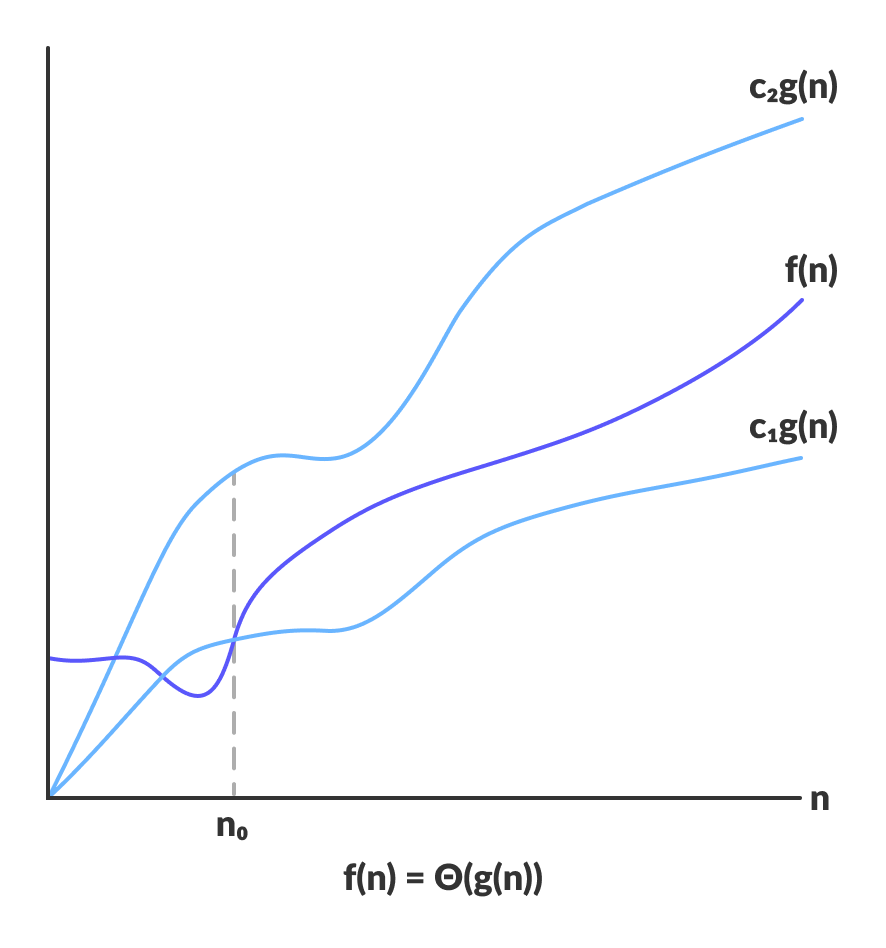
    • अगर किसी फंक्शन f(n) का टाइम कॉम्प्लेक्सिटी Θ(g(n)) है, तो इसका मतलब है कि एक पॉइंट (n₀) के बाद, f(n) हमेशा c₁ · g(n) और c₂ · g(n) के बीच की Band (पट्टी) में रहेगा।
    • Formula: c₁ · g(n) ≤ f(n) ≤ c₂ · g(n) for all n ≥ n₀
  • Example: Merge Sort की कॉम्प्लेक्सिटी हमेशा Θ(n log n) होती है। इसका मतलब है कि इसका Running Time हमेशा n log n के आसपास ही रहेगा, चाहे इनपुट कैसा भी हो।
Theta Graph

Summary (संक्षेप में याद रखें)

Notation Big O (O) Omega (Ω) Theta (Θ)
नाम Upper Bound Lower Bound Tight Bound
केस Worst-Case (सबसे ज़्यादा टाइम) Best-Case (सबसे कम टाइम) Average-Case (बीच का टाइम)
आसान मतलब से ऊपर कभी नहीं जाएगा से नीचे कभी नहीं जाएगा के आसपास रहेगा

यह Notations हमें यह समझने में मदद करते हैं कि हमारा एल्गोरिथ्म Input के बड़े होने पर कितनी तेज़ी से धीमा होता है।

Comments

Post a Comment

Popular posts from this blog

Data Abstraction

Image
What is Data Abstraction? Data Abstraction ka matlab hota hai: “Sirf zaruri cheez dikhana, aur jo andar ki complex working hai usse chhupa dena.” Programming me hum user ko sirf “What to do” dikhate hain aur “How to do it” chhupa lete hain. Isse system simple, secure aur easy-to-use ban jaata hai.     Real-Life Example: TV Remote TV Remote abstraction ka perfect example hai. Aap remote me bas Volume Up , Channel Change , Power jaisa button dabate ho. Aapko nahi pata hota ki andar circuit kaise signal create karta hai, TV tak kaise pahuchta hai, software usse kaise process karta hai. Aapko sirf zaruri functionality dikh rahi hai → This is Abstraction! Agar company remote ki chip badal bhi de, aapka use karna same hi rahta hai. Programming Me Data Abstraction Coding me Data Abstraction ka matlab hota hai ki hum classes aur functions ko aise design karein ki: User ko sirf use karne layak functions dikhaye dein. Un functions ke andar kya logic chal raha hai, woh poora hid...
Read more

Data Abstraction

Image
  What is Data Abstraction? Data Abstraction means showing only the important information to the user and hiding all the internal working details. In simple words: Show what to do . Hide how it works . This makes a system easy to use, clean, and less confusing.   Real-Life Example: TV Remote When you use a TV remote: You only press buttons like Volume Up, Volume Down, or Channel Change. You do not see how the signal travels inside the remote, how the chip works, or how the TV processes the signal. You only see the basic functions. The internal working is hidden. This is called Abstraction . Data Abstraction in Programming In programming, abstraction means that: The user only sees the required functions or methods. The logic inside those functions remains hidden. Example: When you call saveData(data) in a program: You only know that the data will be saved. You do not know whether it is saved using SQL, NoSQL, a file system, or something else. The internal process is hidden fro...
Read more

Data Structure Ka Parichay Aur Prakar (Introduction and Types of Data Structure)

Image
  1. Data Structure Ki Definition Data Structure ek logical aur systematic tareeka hai jisme data elements ko organize kiya jata hai taki essential operations jaise search, add aur delete efficiently kiye ja sake kam time aur memory mein. Simple Example: Ek library ko consider karo. Books (data) ko shelves (data structures) mein unke subjects ke hisaab se arrange kiya jata hai, taki jab aap koi book dhundho to turant mil jaye. 2. Data Structures Ke Prakar Data Structures mainly do categories mein divide hote hain: Primitive aur Non-Primitive . A. Primitive Data Structures Ye basic data types hote hain jo directly machine level par kaam karte hain. Programming languages inhe pre-defined provide karti hain. Integer (int): Poorn sankhyaon ko store karta hai. Example: 10, -5, 1000 Float/Double: Dashmlav sankhyaon ko store karta hai. Example: 3.14, 0.005 Character (char): Single akshar ya symbol store karta hai. Example: 'A', 'z', '9' Boolean (bo...
Read more